Introduction to Computer Programming

In the Computer Sciences, we learn and practice

• writing computer programs
• reading computer programs
• understanding what can and cannot be done
• mapping problems from other domains of computation

How does one write a piece of code to help solve that?

Computational problem solving — the ability to think in computational modes of thought

• Ability to memorize does not help
• What is computational thinking? What is computation? What is thinking?

  • Declarative Knowledge

    • Statements of fact
    • Assertions of truth
    • Axioms

    For example:

    Q: What are square roots?

    A: The square root of x is y such that y squared equals x, and y is positive.

  • Imperative Knowledge

    • Descriptions of how to deduce something
    • How-to knowledge

    For example:

    Q: How does one compute square roots?

    A: Using the Heron-Babylonian method, start with a guess g. If g squared is close to x, stop and the result is g. Otherwise, make a new guess by taking the average of g and x over g, and repeat.

    g_{k+1} = \frac {g_k + x / g_k} {2}

    An iterative Java implementation of the Heron-Babylonian algorithm

    import java.util.Random;
    
    public final class Program {
        final static Random random = new Random();
    
        public static void main(final String[] args) {
            final double value   = 9.0;
            final double epsilon = 0.0000001;
            final double result  = computeSquareRoot(value, epsilon);
            System.out.println("sqrt(" + value + ") ~= " + result);
        }
    
        /**
         * Computes a square root using the Heron-Babylonian algorithm. Passing a
         * negative value for either argument results in -1.
         * 
         * @param x       The value for which the square root is calculated.
         * @param epsilon The value that determines the precision of the calculation.
         * @return        The square root of x with a precision epsilon.
         */
        private static double computeSquareRoot(
                final double x, final double epsilon) {
    
            if (x < 0 || epsilon < 0)
                return -1;
    
            double g = random.nextDouble() * x;
    
            while (Math.abs(x - g * g) >= epsilon) {
                System.out.println("Guess: " + g);
                g = (g + x / g) / 2;
            }
    
            return g;
        }
    }

• Computational thinking — ways to capture a sequence of specific instructions

  • Performed with order (sequence)
  • Performed with conditions — depending on the condition, the subsequent location in the sequence changes
  • Performed with end conditions — something to indicate the sequence has completed and the answer is available

Fixed-program computers

How does one build a mechanical process to capture the set of computations?

• A piece of circuitry designed to do a specific computation

  • a calculator; performs arithmetic
  • Atanasoff, 1941; solves linear equations
  • Alan Turing’s Bombe; breaks German Enigma codes during WWII

• Fixed-program computers is where we started
  Fixed-program computers does not get us to where we want to be.

Interpreter — a stored-program computer

• a machine that can take a recipe as input
• then acts like what is described in that recipe
• has a process that allows a sequence to be executed

Primitive instructions — everything is built using these instructions

• What are the right primitives to use?

  • a known set
  • straight-forward

• Anything described as a process can be captured in the set of primitives.

Turing Compatibility — anything that can be done in one programming language can be done in another programming language

• In 1936, Alan Turing showed that with six simple primitives.
• Anything that could be described in a mechanical process could be programmed.
• For example, “write a value onto a tape.”
• All languages have incorporated these primitives.
• No programming language is better in this sense.

Higher-level abstracts — a broader set of primitives

• We do not start with Turing’s six primitives.
• Goal: describe recipes
  • Describe a sequence of steps built on some primitives.
  • Describe the flow of control that goes through that sequence of steps.

Programming Languages — in order to describe recipes

• There are hundreds, or even more, programming languages.
• They all have their pros and cons.
• Dimensions of programming languages

  • High-level language vs. Low-level language

    • How close are you to the guts of the machine?
    • Richer set of primitives vs. Turing-sized primitives
    • Square root is a primitive vs. Having to code it like we did.
    • Java vs. Assembly

  • General language vs. Targeted language

    • Primitives support a broad range of applications vs. A specific set of applications
    • Java vs. MATLAB

  • Interpreted language vs. Compiled language

    • Interpreter — checker or compiler or both.
    • Interpreter is operating directly on the code at run time.
    • Checkers and compilers create object code, which is executed at run time.
    • Python vs. C

  • Java can be considered interpreted and compiled.

    

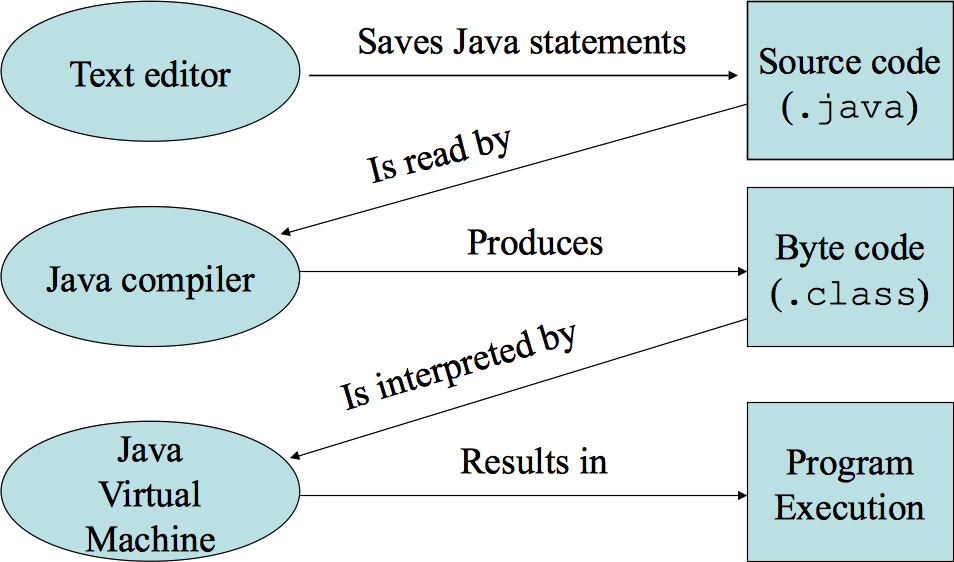
• Reasons for having programming languages

  • To describe recipes, we need to know what the primitives are.
  • We also need to know how to capture things legally.
  • We then need to interact with the computer.

• Syntax vs. Semantics

  • Syntax — the legal expressions in a language
  • Semantics — the meaning of a piece of code

  • Syntax checking

    • System does it for you most of the time
    • Happens at compile time for a compiled language

  • Semantics checking

    • Programmer does it most of the time
    • Happens at run time most of the time

  • Develop a good programming style

    • Defensive programming
    • Murphy’s Law, “Anything that can go wrong will go wrong.”
    • For example, the default case in a switch statement
    • For example, checking whether or not parameters passed by reference are null